Skip to contents

Apply a Butterworth digital filter

Source: R/filter_mnirs.R
filter_butter.Rd

Apply a Butterworth digital filter to vector data with signal::butter() and signal::filtfilt() which handles 'edges' better at the start and end of the data.

Usage

filter_butter(
  x,
  order = 1,
  W,
  type = c("low", "high", "stop", "pass"),
  edges = c("rev", "rep1", "none"),
  na.rm = FALSE
)

Arguments

x

A numeric vector.

order

An integer defining the filter order for method = "butterworth" (default order = 2).

W

A one- or two-element numeric vector defining the filter cutoff frequency(ies) for method = "butterworth", as a fraction of the Nyquist frequency (see Details).

type

A character string indicating the digital filter type for method = "butterworth" (see Details).

"low"

For a low-pass filter (the default).

"high"

For a high-pass filter.

"stop"

For a stop-band (band-reject) filter.

"pass"

For a pass-band filter.

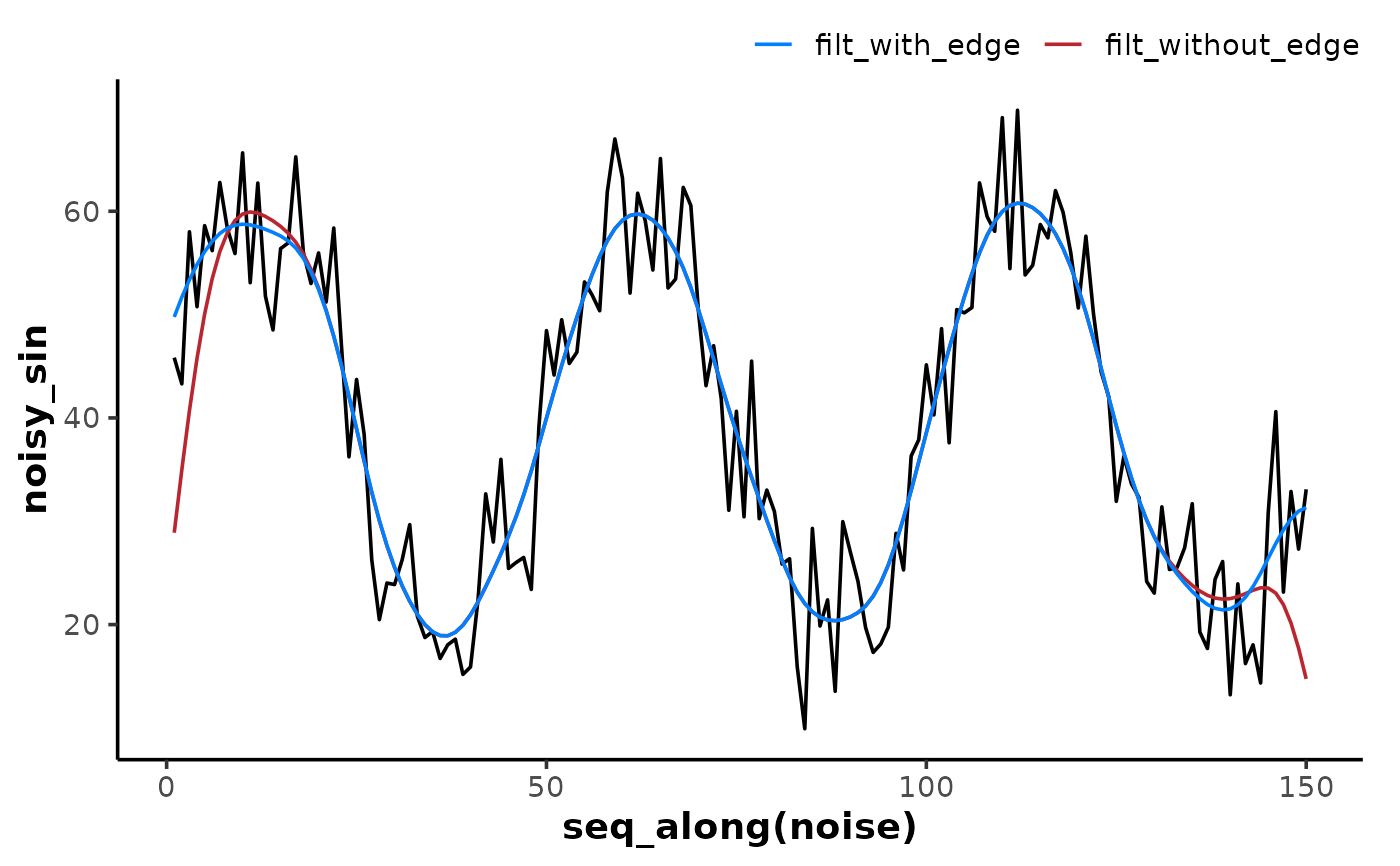
edges

A character string indicating how to pad x for edge detection.

"rev"

(the default) Will pad x with the preceding 5% data in reverse sequence.

"rep1"

Will pad x by repeating the last preceding value.

"none"

Will return the unpadded signal::filtfilt() output.

na.rm

A logical indicating whether missing values should be preserved and passed through the filter (TRUE). Otherwise FALSE (the default) will throw an error if there are any NAs (see Details).

Value

A numeric vector the same length as x.

Details

Applies a centred (two-pass symmetrical) Butterworth digital filter from signal::butter() and signal::filtfilt().

Filter type defines how the desired signal frequencies are either passed or rejected from the output signal. Low-pass and high-pass filters allow only frequencies lower or higher than the cutoff frequency W to be passed through as the output signal, respectively. Stop-band defines a critical range of frequencies which are rejected from the output signal. Pass-band defines a critical range of frequencies which are passed through as the output signal.

The filter order (number of passes) is defined by order, typically in the range order = [1, 10]. Higher filter order tends to capture more rapid changes in amplitude, but also causes more distortion around those change points in the signal. General advice is to use the lowest filter order which sufficiently captures the desired rapid responses in the data.

The critical (cutoff) frequency is defined by W, a numeric value for low-pass and high-pass filters, or a two-element vector c(low, high) defining the lower and upper bands for stop-band and pass-band filters. W represents the desired fractional cutoff frequency in the range W = [0, 1], where 1 is the Nyquist frequency, i.e., half the sample rate of the data in Hz.

Missing values (NA) in x will cause an error unless na.rm = TRUE. Then NAs will be preserved and passed through in the returned vector.

See also

signal::filtfilt() signal::butter()

Examples

library(ggplot2)

set.seed(13)
sin <- sin(2 * pi * 1:150 / 50) * 20 + 40
noise <- rnorm(150, mean = 0, sd = 6)
noisy_sin <- sin + noise
filt_without_edge <- filter_butter(x = noisy_sin, order = 2, W = 0.1, edges = "none")
filt_with_edge <- filter_butter(x = noisy_sin, order = 2, W = 0.1, edges = "rep1")

ggplot(data.frame(), aes(x = seq_along(noise))) +
    theme_mnirs() +
    scale_colour_mnirs(name = NULL) +
    geom_line(aes(y = noisy_sin)) +
    geom_line(aes(y = filt_without_edge, colour = "filt_without_edge")) +
    geom_line(aes(y = filt_with_edge, colour = "filt_with_edge"))